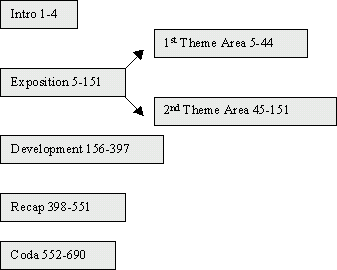
Analysis of Symphony No. 3 in e-flat Major (eroica), Op. 55
3/19/1999

Beethoven°s third symphony was written during the years of 1803 and 1804. At that point it was probably the longest symphony ever written. It consists of 4 movements as shown below. It is interesting to note that the key structure of the work as a whole mirrors the key structure of sonatina form.

Beethoven°s symphonies make use of an expanded orchestra. In this work he adds 2 clarinets and 1 horn to the standard Mozart orchestra. He also writes separate parts for the cellos and basses, but they are still written on the same staff. In later symphonies he would add trombones.

Below is the instrumentation for this symphony.

The first movement is in eb. After the short introduction the first theme area begins. This continues to measure 45 where an F major chord (V of V in Bb) helps to establish the new key area. The exposition is repeated before beginning the development. The development section introduces some new material at measure 284. This new material borrows part of its rhythm from the beginning of the secondary theme area. The recapitulation occurs from 398 to 551 followed by a coda section. In the coda the new material that was introduced in measure 284 returns. The movement finishes with a very strong V to I cadence in eb major.

Below is a diagram of the movement:

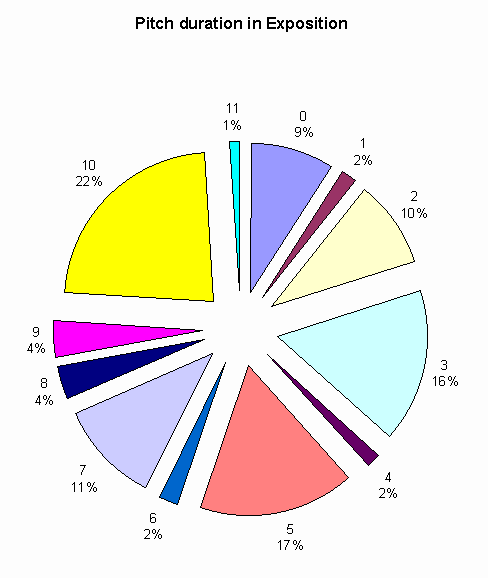
My analysis of the exposition is statistical in nature. My hypothesis is that the different theme areas should be recognizable by analyzing the total duration of sounding pitches on a measure by measure basis. To facilitate this type of analysis, a method was needed to represent the notes as numerical data. Four pieces of information were recorded about each note: measure number, pitch, duration, and instrument. For this analysis the instrument data was not needed, but it helped reduce the number of errors in the entry process.

To record the pitches octave displacement was ignored, but transposing instruments were taken into account. each sounding chromatic pitch was assigned a number (C=0, C#/Db=1, D=2 etc.). Note spelling was ignored. Duration was recorded with a value of an eighth note equaling one. This means that a quarter note has a duration of 2, a half note has a duration of 4, etc. Two notes sounding at the same time, but two of the same instruments were counted as separate occurrences of that pitch. For example: If both clarinets play a quarter note middle C in a certain measure, then the total duration for middle C in that measure will be 4 (2 duration X number of instruments). The exception to this is the cello and bass parts. Because strings usually function together as one instrument, the cello and bass parts were not treated separately in places where they play the same pitches. Octave displacement is still ignored. For example: If the cello part plays middle C and the bass part plays the C sounding an octave lower, the analysis will consider there to be only one occurrence of the pitch C.

All this data was entered into a spreadsheet and produced over 3000 records. This spreadsheet will not be included in this paper because it contains only information available in the score. Once the data entry was complete identical pitches were grouped together and their sum calculated by measure. This produced a new spreadsheet showing the total duration for each pitch in columns with measures represented by rows. This spreadsheet is included at the end of this paper.

First we will consider the exposition as a whole. Below is a graph showing the total duration of each pitch in the exposition.

At first it seems surprising that Bb (10) is the note with the highest occurrence. One would think that eb (3) would come in first. However, since the note Bb is part of an eb major triad as well as a Bb major triad, it is logical that its total duration should be more than that of eb.

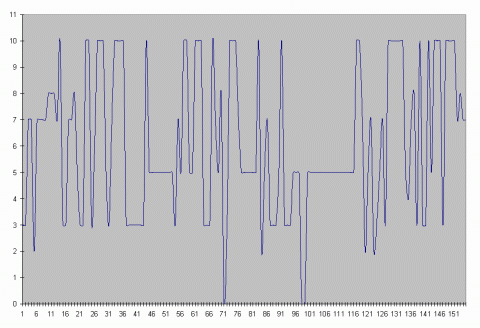
Now we will look at how the exposition moves through time. The graph below shows the pitch with the longest duration in each measure. Most of the measures favor either eb (3) or Bb (10). One exception to this is right around measure 45 where F (5) is the predominate note. From our previous discussion of this movement we know that is where the V of our second key area takes us to Bb.

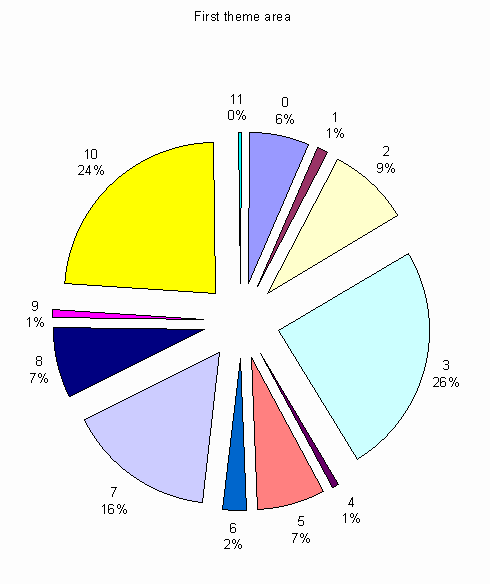
The following graph shows the pitch durations for the first theme area (1-44). Notice that the top three notes are eb (3) Bb (10) and G (7). As expected these are the notes from an eb major triad.

The following graph covers measures 45 to 155. The top 3 pitches are Bb (10) F (5) and eb (3). The eb comes as a surprise. One would expect to see the 3^rd of Bb (D). The eb beats D in this graph because it is used often in F7.